ACL 2019论文 Sparse Sequence-to-Sequence Models,代码实现 entmax。
稀疏序列到序列模型
论文概述
(一)直观看论文的工作:修改了softmax计算方式,变成了稀疏的softmax,使得在某一阈值下的数值都变成了0。
(二)本文中稀疏的softmax用在了下面两个地方:
- seq2seq在解码输出层的softmax
- attention中的softmax。
(三)为什么要用稀疏softmax?
从多标签分类角度:稀疏化Softmax的输出能更适合处理多标签问题。这里首先明确两个概念:多标签分类(multi-label classification)问题和多分类(multi-class classification)问题。多标签分类问题面对的实例可以属于多个标签,例如,一部电影可以是“韩国”、“动作”、“惊悚”。机器翻译的解码阶段,我也认为是个多标签分类问题,因为同一个单词在上下文语境的翻译也可以是多个。而多分类问题指的是一个实例有且仅属于多个分类中的一个。例如,手写数字识别,一张图片对应0~9中唯一一个数字。根据Softmax函数的形式化定义可知,Softmax函数更适合定义多分类问题。那么,为了转换Softmax函数的形式,使之适合多标签分类问题,就产生了sparsemax。
从Attention角度:Attention的关键是映射函数,它对输入元素的相对重要性进行编码,将数值映射为概率。而常用的关注机制Softmax会产生密集的注意力。因为softmax的输出都大于0,故其输入的所有元素对最终决策都有或多或少的影响。
实际工作中遇到的问题:两个语句的语义对齐,出现不该对齐的部分也对齐了的情况(参考上面图)
前人工作介绍
为了克服softmax这种缺点,Martins发表的论文 From Softmax to Sparsemax:A Sparse Model of Attention and Multi-Label Classification 提出了能够输出稀疏概率的Sparsemax,这能为Attention提供更多的解释性。
sparsemax的定义
假设 $\Delta d :=\{p\in \mathbb{R}^d: p\geqslant 0, ||p||$ 表示维度为d的概率向量,softmax可以看成是从$\mathbb{R}^d$到$\Delta d$的映射中的一个。则sparsemax可以定义成另一种形式的softmax,其特点是产生稀疏的概率分布:$sparsemax(z) := argmin_{p\in \Delta ^d} ||p-z||^2$。可以看到它的预测的分布满足:$p^* := sparsemax(z)$,很容易将低分数的元素置为0。
- 对比softmax形式$softmax(z)=exp(z_i)/\sum _j(exp(z_j))$,首先Sparsemax的目标是直接逼近真实的多标签分类分布,另外Sparsemax不再由指数函数对输出z做smooth变换。采用直接将输出z投影到单纯形的方式能够起到输出的稀疏化效果
sparsemax的物理意义等价于将输出z投影到单纯形上,投影的方式为通过欧式距离找到距离单纯形上最近的一点,其投影点为p。由于单纯形的限制,导致这个投影点会大概率(相对于d维空间单纯形很小)落在单纯形的边界上,从而导致了稀疏化的效果。例如,在下图的例子中,当2维空间中的投影点落在单纯形的边界上时即形成了稀疏化的输出结果。

sparsemax的求解
Sparsemax的函数形式在真实分布未知的情况下并不能直接求解。通过拉格朗日法得到它的对偶形式:$L(z, \mu , \tau ) = \frac{1}{2}||p-z||^2-\mu^Tp+\tau (1^Tp-1)$,求解得:
$Sparsemax(z) = [z_i- \tau(z)], s.t. \sum_j[z_j-\tau(z)]_+=1$
$[t]_+=max\{0,t\}$
$\tau(z)=(\sum_{j\leq k(z)}z(j)-1)/k(z)$
$k(z)=max\{k\in[K]|\sum_{j\leq k}z(j) < 1+kz_{(k)}\}$
$z_{(1)} \geq z_{(2)} \geq …\geq z_{(k)}$
其中[K]表示K个标签对应的下标集合。
用语言形式描述Sparsemax的求解过程:
- 将输出z按值降序排列
- 按序比较条件$\sum_{j\leq k}z(j) < 1+kz_{(k)}$,若不满足则退出,求得满足条件的输出数k(z)
计算$\tau(z)$并得到sparsemax
这里的$\tau(z)$也被称作关于z的阈值函数。通过在2维和3维空间上的示意图可以看到Sparsemax和Softmax的基本性质基本相同,在Sparsemax上基本保持了Softmax上的序关系,不同的是Sparsemax的输出不再平滑,头尾都被“截断”了。

sparsemax的损失函数和梯度
[注]:以下内容在Martins论文中和本篇论文中公式的形式不一样,下面的公式都是本篇论文中给出的。
sparsemax的损失函数可以定义为:$L_{sparsemax}(y,z):=\frac{1}{2}(||e_y-z||^2-||p^*-z||^2)$,其中$e_y:=[0,…,1,0,…,0]$是真实标签。
- Sparsemax的损失函数是一个处处可导的凸函数。
- 对比Softmax,Softmax函数的负对数似然损失为$L_{softmax}=-\sum_{i=1}^My_ilog \frac{e^{zi}}{\sum _ke^{zk}}$
- Sparsemax函数由于存在截断点,由于截断点的梯度不连续,有在截断点处的梯度不连续,被截断部分(值为0)的对数似然无法计算等问题,导致Sparsemax无法计算。因此文章提出了处处可导的凸函数。
- $L_{sparsemax}(y,z)$在z上是连续可微,且存在性质:$L_{sparsemax}$ 为0,当且仅当对任意$y\neq y’$,有$z_y \geqslant z_{y’} +1$。(即有一个margin,可参考:Softmax理解之margin)
训练模型使用sparsemax的loss时,其梯度为:$\bigtriangledown _zL_{sparsemax}(y,z)=-e_y+p^*$。
对这个梯度公式的直观理解:用到的部分回传梯度,没用到的部分梯度为0
将sparsemax运用于attention机制中时,可以发现sparsemax在任意处都是可导的(Martins论文中已证):
$\frac{\partial sparsemax(z)}{\partial z}=diag(s)-\frac{1}{||s||_1}ss^T$,
其中当$0 < p^*_j$时,$s_j=1$,否则$s_j=0$。
本文主要贡献
从熵的角度定义了一簇sparsemax
从“熵”角度解释sparsemax
为了理解sparsemax,我们可以从另一个角度理解softmax:
$softmax(z) = argmax_{p\in \Delta d}(p^Tz) + H^S(p)$$H^S (p) :=\sum _jp_jlogp_j$
后者是著名的Gibbs-Boltzmann-Shannon entropy。
同样的去理解sparsemax:
$sparsemax(z) = argmax_{p\in \Delta d}(p^Tz) + H^G(p)$
$H^G (p) :=\frac{1}{2}\sum _jp_jlog(1-p_j$
后者是Gini entropy。
因此,softmax和sparsemax只是在entropy的正则项上不同。
通过 定义的一系列的熵Tsallis
定义的一系列的熵Tsallis
$Tsallis \alpha -entropies$:
$H^T_\alpha (p) := \left\{\begin{matrix}
\frac{1}{\alpha (\alpha -1)}\sum _j(p_j-p^\alpha _j) & \alpha \neq 1\
H^S(p) & \alpha= 1
\end{matrix}\right.$
这个熵家族是连续的:对于任意$p \in \Delta d$,有:
$lim_{\alpha \rightarrow 1}H^T_\alpha (p)=H^S(p)$,
$H^T_2\equiv H^G$
也就是说Tsallis熵在Shannon和Gini之间。
由Tsallis熵定义entmax
entmax定义:
$\alpha-entmax(z):=argmax_{p\in\Delta^d}p^Tz + H^T_\alpha (p)$
$p^* := \alpha-entmax(z)$
损失函数:
$L_\alpha (y,z):=(p^-e_y)^Tz+H^T_\alpha (p^)$
其梯度:
$\bigtriangledown _zL_\alpha (y,z)=-e_y+p^*$
可以知道,$1-entmax \equiv softmax$,$2-entmax \equiv sparsemax$,$L_1$是负对数似然,$L_2$是sparsemax loss。对于任意$1 < \alpha$ entmax可以产生稀疏的概率分布,如下图:

- Tsallis熵损失函数是可导的,且有一个性质:当正确分类的得分比其他错误分类的得分多出$\frac{1}{\alpha -1}$以上时,损失变成是0。这对于seq2seq模型来说,解码器在非常容易进行解码的时间步上,会作出非常确定的预测,当有若干个可能的候选时,会有稀疏的不确定性。
计算 $p^* = \alpha -entmax(z)$
对于$\alpha=1$,有:$softmax(z)_j:=\frac{exp(z_j)}{\sum _iexp(z_i)}$。
对于$1<\alpha<2$,有:$\alpha -entmax(z)=[(\alpha -1)z-\tau 1]^{1/\alpha -1}_+$(对于$z_j\leq \tau / \alpha -1$的分数为0)
对于$\alpha=2$,则是在$\Delta ^d$上的欧几里得投影。
可以使用两种算法计算
:
基于排序

可参考root_finding中第79~129行。
- 基于分治法

可参考activations中第214~244行
实验结论
单词变形任务上的准确率(多语言)

英德翻译任务上的BLEU

英德翻译任务上不同的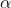 产生的稀疏性
产生的稀疏性

相比于softmax,1.5-entmax有更少的输出但有更高的BLEU,sparsemax虽然输出更稀疏,但BLEU指标不如1.5-entmax。在attention和softmax输出中不同的取值,对于验证集准确率的影响可参考下图:

在翻译任务上用1.5-entmax产生的attention可视化如下:

在翻译任务上,softmax和1.5-entmax在训练时间上的比较:

总结
目前attention受到关注,产生的很多稀疏的attention的计算方法,本文直接改变了softmax的计算方式,使其归一化的结果更为稀疏,对未来的研究有参考价值。